关键词 Variational Message Passing, Bayesian networks, Exponential Family, Sufficient Statistics.
传统的变分贝叶斯方法对模型的推导是繁琐而复杂的。J. Winn, Bishop [1] [2] 考虑了贝叶斯网络中的共轭指数网络 (conjugate-exponential networks) 提出变分消息传播 (VMP, Variational Message Passing) 。这种方法使得充分统计量与自然参数都有一个标准形式,现在该方法已经取代了手工推导, 成为标准的变分贝叶斯推断方法。而对于非共轭指数网络 (比如混合模型) ,也能通过进一步的近似转化为标准形式。
理论基础
Bayesian networks
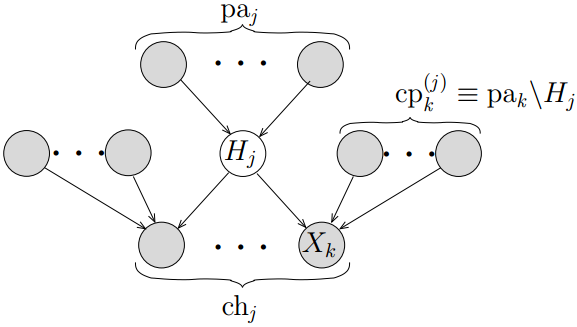
变分信息传播方法是建立在贝叶斯网络[3]上的,如图所示,对于一个节点\({H_j}\),它的父节点为\(p{a_j}\),子节点为\(c{h_j}\), 子节点\({x_k}\)的父节点为\(cp_k^{(j)} \equiv p{a_k}\backslash {H_j}\)。所有节点统称为\({H_j}\)的马尔科夫毯,对于变分贝叶斯推理, 我们只需要关心这个模型,\(H\)为参数或潜在变量,其父节点为它的超参数,子节点为数据样本, co-parents为其他参数或潜在变量。
Exponential Family
设\((X,B\|{p_\theta }:\theta \in \Theta \|)\)是可控参数统计结构,其密度函数可表示为如下形式:
\[p_{\theta}(x) = c(\theta) \exp \{ \sum\limits_{i = 1}^k c_j(\theta ){T_j}(x) \} h(x)\]并且它的支撑\(\{ x:{p_\theta }(x) > 0\}\)不依赖于θ,则称此结构为指数型的统计结构,简称指数结构,其中的分布族为指数分布族。 \(0 < c(\theta ),{c_1}(\theta ),...,{c_k}(\theta ) < \infty ,{T_j}(x)\)都与θ无关,且取有限值的B可测函数,k为正整数,\(h\left( x \right) > 0\),常见指数分布族,如二项分布,二元正态分布,伽马分布。
对于一个条件分布,如果它能写成如下形式,则称它属于指数分布族,
\[P(X\|Y) = \exp [\phi {(Y)^T}u(X) + f(X) + g(Y)]\]其中\(\phi (Y)\)称为自然参数 (natural parameter) 向量,\(u(X)\)称为自然统计 (natural statistic) 向量。\(g(Y)\)作为归一化函数使得对于任意的Y都能整合到统一的形式。指数分布族的好处是它的对数形式是可计算的并且它的状态可以用自然参数向量所概括。
Conjugate-Exponential Model
当变量X关于父节点Y的条件概率分布P(X|Y)为指数分布族,且为父节点分布P(Y)的共轭先验,那么称这样的模型是共轭指数模 (Conjugate-Exponential Model) 。 考虑共轭指数模型,其后验的每个因子与它的先验都有相同的形式,因而只需要关心参数的变化,而无需整个函数。所谓相同的形式是指属于同样的分布, 比如都属于正态分布,伽马分布,多项式分布等。
Sufficient Statistics
如果知道自然参数向量\(\phi (Y)\),那么就能找到自然统计量的期望。重写指数分布族,用\(\phi\)作为参数,\(g\)重新参数化为\(\tilde g\)则,
\[P(X\|\phi ) = \exp [{\phi ^T}u(X) + f(X) + \tilde g(\phi )]\]对\(X\)积分有,
\[\int_X {\exp [{\phi ^T}u(X) + f(X) + \tilde g(\phi )]} dX = \int_X {P(X\|\phi )dX} = 1\]然后对\(\phi\)微分,
\[\begin{align*} \int_X {\frac{d}\exp [{\phi ^T}u(X) + f(X) + \tilde g(\phi )]} dX &= \frac{d}{ d\phi}(1) = 0\\ \int_X P(X \|\phi)\left[ u(X) + \frac{d\tilde g(\phi )}{d\phi} \right] dX &= 0 \end{align*}\]得自然统计量的期望,
\[\left\langle u(X) \right\rangle _{P(X\|\phi )} = - \frac{d\tilde g(\phi )}{d\phi} \tag{1}\]变分消息传播模型
变分分布Q在共轭指数模型下的最优化
不失一般性,考虑变分分布的一个因子\(Q\left( Y \right)\), \(Y\)为马尔科夫毯上一个节点,子节点为\(X\),如图-2所示
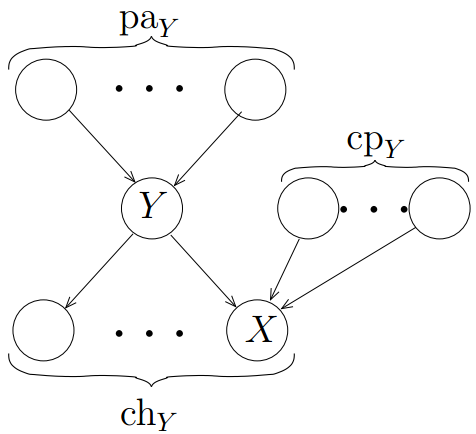
根据指数族条件分布的一般形式,则变量Y关于父节点的条件概率为,
为了更新Q(Y),需要找到(2),(3)关于除Y外其他因子的期望。对任何指数族的自然统计量u的期望都可以用自然参数向量ϕ带入 (2-19) 式得到。即对于任何变量A,都可以找到\({\left\langle u_A(A) \right\rangle _Q}\)。特别的,当A为被观测量时,我们能直接计算得\({\left\langle {u_A(A)} \right\rangle_Q} = u_A(A)\)。
从(3),(4)式可以看出\(\ln P(X\|Y,c{p_Y})\)与\(u_X(X),u_Y(Y)\)分布成线性关系。而共轭要求对数条件分布也会与所有的\({u_Z}(Z)\)成线性,\(Z \in c{p_Y}\)。因而看得出\(\ln P(X\|Y,c{p_Y})\)是一个关于u的多线性函数。
考虑Y的变分更新方程,
\[\begin{align} \ln Q_Y^*(Y) &= {\left\langle \phi_Y{(p{a_Y})^T}u_Y(Y) + {f_Y}(Y) + g_Y(p{a_Y}) \right\rangle _{\sim Q(Y)}} \\ &\quad +\sum\limits_{k \in c{h_Y}} \left\langle \phi_{XY}{(X,c{p_Y})^T}u_Y(Y) + \lambda (X,c{p_Y}) \right\rangle_{\sim Q(Y)} + const. \\ &= {\left[ {\langle \phi_Y{(p{a_Y})} \rangle}_{\sim Q(Y)} + \sum\limits_{k \in ch_Y} {\langle \phi_{XY{(X,cp_Y)}} \rangle }_{\sim Q(Y)} \right]^T}{u_Y(Y)} + {f_Y}(Y) + const.\\ &= \left[ {\phi_Y^*} \right]^T u_Y(Y) + {f_Y}(Y) + const.\\ \end{align}\]其中,
\[\phi_Y^* = \left\langle {\phi_Y{(p{a_Y})^T}} \right\rangle _{\sim Q(Y)} + \sum\limits_{k \in c{h_Y}} \left\langle {\phi_{XY}{(X,c{p_Y})^T}} \right\rangle_{\sim Q(Y)} \tag{2}\]正如以上所解释的,\(\phi_Y\)和\(\phi_{XY}\)的期望都是相应的自然统计向量期望的多线性函数。因而有可能将以上期望重新参数化为
\[\tilde{\phi_Y}\left( \left\{ \left. \left\langle u_i \right\rangle \right\} \right._{i \in p{a_Y}} \right) = \left\langle \phi_Y(p{a_Y}) \right\rangle\] \[\tilde{\phi_{XY}}(\langle u_X\rangle ,\{\langle u_j \rangle\}_{j \in cp_Y}) = \langle \phi_{XY}(X,c{p_Y}) \rangle\]举例:
如果X服从\(N(Y,{\beta ^{ - 1}})\),那么
\[\begin{equation} \begin{split} \ln P(X\|Y,\beta ) & = {\left[ \begin{array}{l}\beta Y\\ - \beta/2\end{array} \right]^T}\left[ \begin{array}{l}X{X^2}\end{array} \right] + \frac{1}{2}(\ln \beta - \beta {Y^2} - \ln 2\pi)\\ & = {\left[ \begin{array}{l}\beta X\\- \beta /2\end{array} \right]^T}\left[ \begin{array}{l}Y{Y^2}\end{array} \right] +\frac{1}{2}(\ln \beta - \beta {X^2} - \ln 2\pi )\\ & = {\left[ \begin{array}{c}-\frac{1}{2}(X - Y)^2\\\frac{1}{2} \end{array}\right]^T}\left[\begin{array}{l} \beta\\\ln \beta\end{array} \right] - \frac{1}{2}\ln 2\pi \end{split} \end{equation}\]其中\(u_X(X) = \left[ \begin{array}{l}X\\{X^2}\end{array} \right]\),\(u_Y(Y) = \left[ \begin{array}{l}Y\\{Y^2}\end{array} \right]\),\({u_\beta}(\beta) = \left[ \begin{array}{l}\beta \\\ln \beta \end{array} \right].\)
\(\phi_{XY}(X,\beta ) = \left[ \begin{array}{l}\beta X\\ - \beta /2\end{array} \right]\)可以重参数化为\({\tilde{\phi} _{XY}}(\langle u_X \rangle ,\langle {u_\beta} \rangle ) = \left[ \begin{array}{l} \langle {u_\beta} \rangle_{0} \langle u_X \rangle_{0} \\ - \langle {u_\beta} \rangle_{0} /2 \end{array} \right]\)
其中\(\langle {u_\beta} \rangle_{0}\)和\(\langle u_X \rangle_{0}\)分别表示\(\langle {u_\beta} \rangle\)和\(\langle u_X \rangle\)的第一个元素。
变分消息传播模型
在贝叶斯网络中,由于Q可因式分解,则有
\[\begin{align*} L(Q) &= \left\langle {\ln P(H,V)} \right\rangle - \left\langle {Q(H)} \right\rangle\\ &= \sum\limits_i {\left\langle {\ln P({X_i}\|p{a_i})} \right\rangle - \sum\limits_{i \in H} {\left\langle {\ln {Q_i}({H_i})} \right\rangle } } \\ &\overset{\text{def}}{=} \sum\limits_i L_i \end{align*}\]\(L\left( Q \right)\)被分解为每一个节点上的贡献值 \(\left\{ L_i \right\}\),如节点\({H_j}\)的贡献值为
\[\begin{align*} {L_j} &= \left\langle {\ln P({H_i}\|p{a_j})} \right\rangle - \left\langle {\ln {Q_i}({H_i})} \right\rangle\\ & =\langle {\phi _j}(p{a_j})^T \rangle \langle u_j(H_j) \rangle + \langle {f_j}(H_j) \rangle + \langle g_j(p{a_j}) \rangle - \left[ {\phi _j^*}^T \langle u_j(H_j) \rangle + \langle {f_j}(H_j) \rangle + \tilde{g}_j(\phi _j^*) \right]\\ & ={\left( {\langle {\phi_j(p{a_j})} \rangle - \phi _j^*} \right)^T}\langle {u_j({H_j})} \rangle + \langle {g_j(p{a_j})} \rangle - \tilde{g}_j(\phi _j^*) \end{align*}\]注意到\(\left\langle {\phi_j(p{a_j})} \right\rangle\)和\(\phi _j^*\)在求\({H_j}\)的后验分布时就已经计算了;\(\left\langle {u_j({H_j})} \right\rangle\)在\({H_j}\)传出消息的时候也已经计算了,这样降低了下界的计算成本。
特别地,对于每个观测变量\({V_k}\)对下界的贡献值则更简单,
\[{L_k} = \left\langle {\ln P({V_k}\|p{a_k})} \right\rangle = {\left\langle {\phi_j(p{a_j})} \right\rangle ^T}{u_k}({V_k}) + {f_k}({V_k}) + {\tilde g_k}\left( {\left\langle {\phi_j(p{a_j})} \right\rangle } \right)\]变分消息传播算法
变分消息的定义
来自父节点的消息 (Message from parents) :父节点传播给子节点的消息只是自然统计量的期望:
\(\begin{equation} m_{Y \to X} = \left\langle {u_Y}\right\rangle. \end{equation} \tag{3}\)
消息传播给父节点 (Message to parents) :依赖于X之前从Y的co-parents接收到的消息;对任何节点A,如果A是被观测量,那么\(\left\langle {u_A} \right\rangle = u_A\),
\[m_{X \to Y} = \tilde{\phi}_{XY}\left( \left\langle u_X \right\rangle ,{\left\{ m_{i \to X} \right\}}_{i \in c{p_Y}} \right) \tag{4}\]用Y接收来自父节点与子节点的所有消息来计算\(\phi_Y^*\),然后我们就能通过计算更新后的自然参数向量\(\phi_Y^*\)来找到Y的更新后的后验分布\(Q_Y^*\),\(\phi_Y^*\)的计算公式如下,
\(\phi_Y^* = \tilde{\phi_Y}\left( \left\{ m_{i \to Y} \right\}_{i \in p{a_Y}} \right) + \sum\limits_{j \in c{h_Y}} m_{j \to Y} \tag{5}\).
该式与 (2) 式一致。从 (1) 式可以看出自然统计量的期望\({\left\langle {u_Y} \right\rangle _{Q_Y^*}}\)是\(Q_Y^*\)的单一函数,这样我们就可以用它来计算期望的新值。变分消息传播算法通过迭代的消息传播来最优化变分分布Q.
算法描述
| Step1. 通过初始化相关的矩向量\(\left\langle {u_j({X_j})} \right\rangle\)来初始化每个因子分布\({Q_j}\). |
| Step2. 对于每一个节点\({X_j}\), |
| 1) 从父节点和子节点接收 (3),(4) 式所定义的消息。 前提是子节点已经从\({X_j}\)的co-parents接收到消息。 |
| 2) 使用 (5) 式更新自然参数向量\(\phi _j^*\); |
| 3) 根据新的参数向量更新距向量\(\left\langle {u_j({X_j})} \right\rangle\); |
| Step3. 计算新的下界\(L(Q)\); |
| Step4. 如果经过数次迭代已经无法增加下界值,或者各边缘分布达到稳定值,则结束;否则回到Step2。 |
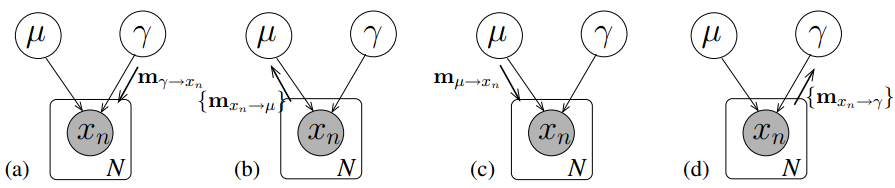
举例:对于单一高斯模型消息传播过程如下图
混合模型
到目前为止只考虑了来自指数族的分布。而通常来讲,混合模型并非来自指数族,比如高斯混合模型,通常需要将混合分布转化为指数族分布形式。
考虑高斯混合模型,通常有如下形式,
\[P(X\|\{ \pi_k\} ,\{ \theta_k\} ) = \sum\limits_{k = 1}^K {\pi_kP_k(X\|\theta_k)}\]可以引入一个离散型潜在变量λ,表示每个观测点是属于哪个单高斯分布。重写分布函数为:
\[P(X\|\lambda ,\{ \theta_k\} ) = \sum\limits_{k = 1}^K P_k{(X\|\theta_k)}^{\delta_{\lambda k}}\]加入该λ变量后该分布属于指数分布族,可写成
\[\ln P(X\|\lambda ,\{ \theta_k\} ) = \sum\limits_k {\delta (\lambda ,k)\left[ {\phi_k{(\theta_k)^T}{u_k}(X) + {f_k}(X) + {g_k}(\theta_k)} \right]}\]如果X有子节点Z,那么共轭条件要求每一个成分都有相同的自然统计向量, 统一定义为\({u_1}(X) = {u_2}(X) = ... = {u_K}(X)\overset{\text{def}}{=}u_X(X)\)。 另外,我们可能要使模型的其他部分也有相同的形式,虽然不要求共轭,即\({f_1} = {f_2} = ... = {f_K}\overset{\text{def}}{=} {f_X}\)。 在这种情况下,混合模型的每个成分都有相同的形式,可写成,
\[\begin{align*} \ln P(X\|\lambda ,\{ \theta_k\} ) &= {\left[ {\sum\limits_k {\delta (\lambda ,k)\phi_k(\theta_k)} } \right]^T}u_X(X) + {f_X}(X) + \sum\limits_k {\delta (\lambda ,k){g_k}(\theta_k)}\\ &={\phi _X}{(\lambda ,\{ \theta_k\} )^T}u_X(X) + {f_X}(X) + {\tilde g_X}({\phi _X}(\lambda ,\{ \theta_k\} )) \end{align*}\]其中定义\({\phi _X} = \sum\limits_k {\delta (\lambda ,k)\phi_k(\theta_k)}\)。这样对于每个成分来说条件分布都有了 与指数分布族一样的形式,便可以应用变分消息传播算法。
从某个节点X传播个子节点的消息为\(\left\langle {u_X(X)} \right\rangle\),而这是通过混合参数向量\({\phi _X}(\lambda ,\{ \theta_k\} )\)计算的。 相似地,节点X到父亲节点\(\theta_k\)的消息是那些以它为父节点的子节点发出的,而节点X中哪些属于\(\theta_k\)是由指标变量\(Q(\lambda = k)\)的后验确定的。最后,从X到的消息是一个K维向量,其中第k个元素为\(\left\langle {\ln P_k(X\|\theta_k)} \right\rangle\).
算法分析
VB算法与EM算法比较
EM算法计算随机变量 (或归类于参数) 后验分布的点估计,但估计隐变量的真实后验分布。用这些参数的众数作为点估计,无任何其他信息。 而在VB算法作为一个分布估计 (Distributional Approximation) 方法,计算所有变量的真实后验分布的估计,包括参数和隐变量。 在贝叶斯推断中,计算点估计一般使用常用的均值而非众数。与此同时,应该注意的是计算参数在VB中与EM有不同的意义。 EM算法计算贝叶斯网络本身的参数的最优值。而VB计算用于近似参数和隐变量的贝叶斯网络的参数最佳值,VB会先找一个合适的参数分布, 通常是一个先验分布的形式,然后计算这个分布的参数值,更准确说是超参数,最后得到联合分布的各参数的分布。
算法复杂性
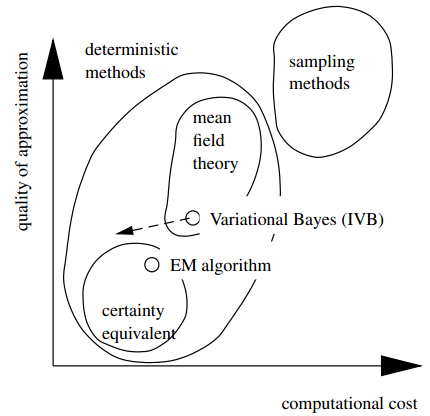
变分贝叶斯估计方法是众多概率函数估计技术之一。还有许多其他被广泛使用的估计算法,一般分为确定性 (deterministic) 和随机性 (stochastic) 的方法,比如基于点估计的极大似然估计、极大后验概率估计,基于局部估计的Laplace估计,基于spline估计的B-样条估计,还有经验性估计,利用随机采用的如MCMC方法。变分贝叶斯方法作为平均场估计,能够在计算复杂度和精度之间保持一个良好的关系,如图-4所示。变分贝叶斯方法主要的计算压力在于它的IVB算法——一系列为求取变分边缘概率相关的矩估计而进行的迭代。如果只关心计算代价而对精度要求不高,那么可以用简单的估计方法来代替变分边缘概率,或者减少估计迭代的次数,这样变分估计的路径将沿着虚线往下。
小结
本文对基于贝叶斯网络的变分消息传播方法从理论基础到算法流程展开论述。 特别地与EM算法进行比较,分析了变分贝叶斯方法的算法复杂性。 下一篇将给出高斯混合模型的例子,以及MATLAB实现源代码。
参考文献
[1] John M. Winn, M. Bishop, Variational Message Passing, Journal of Machine Learning Research, 2004
[2] John M. Winn, Variational Message Passing and its Applications, University of Cambridge, 2003
[3] Michael I. Jordan, An Introduction to Variational Methods for Graphical Models, Machine Learning, 1999
完整文章下载: [pdf]